Cumulative Risk and Long Covid
The statistics of gambling with reinfection in the shadow of long term disease
In light of recent Statistics Canada data on Long Covid prevalence in Canada, and the recent re-sharing of WHO comments on increased likelihood with increased reinfection, I felt it would be prudent to revisit the concept of cumulative risk.
Oh, and grab a die 🎲 and keep it handy.
Endemicity evangelicals would have you believe that with increasing variance comes decreasing virulence and the transition of SARS-CoV-2 to a seasonal illness we all safely contract multiple times per year.
If we take this at face value, how does it play out?
Before we continue, it bears stating that the concept of guaranteed decreasing virulence is bunk. While we are fortunate that Omicron has been less severe than previous variants, its contagiousness has left orders of magnitude more dead.
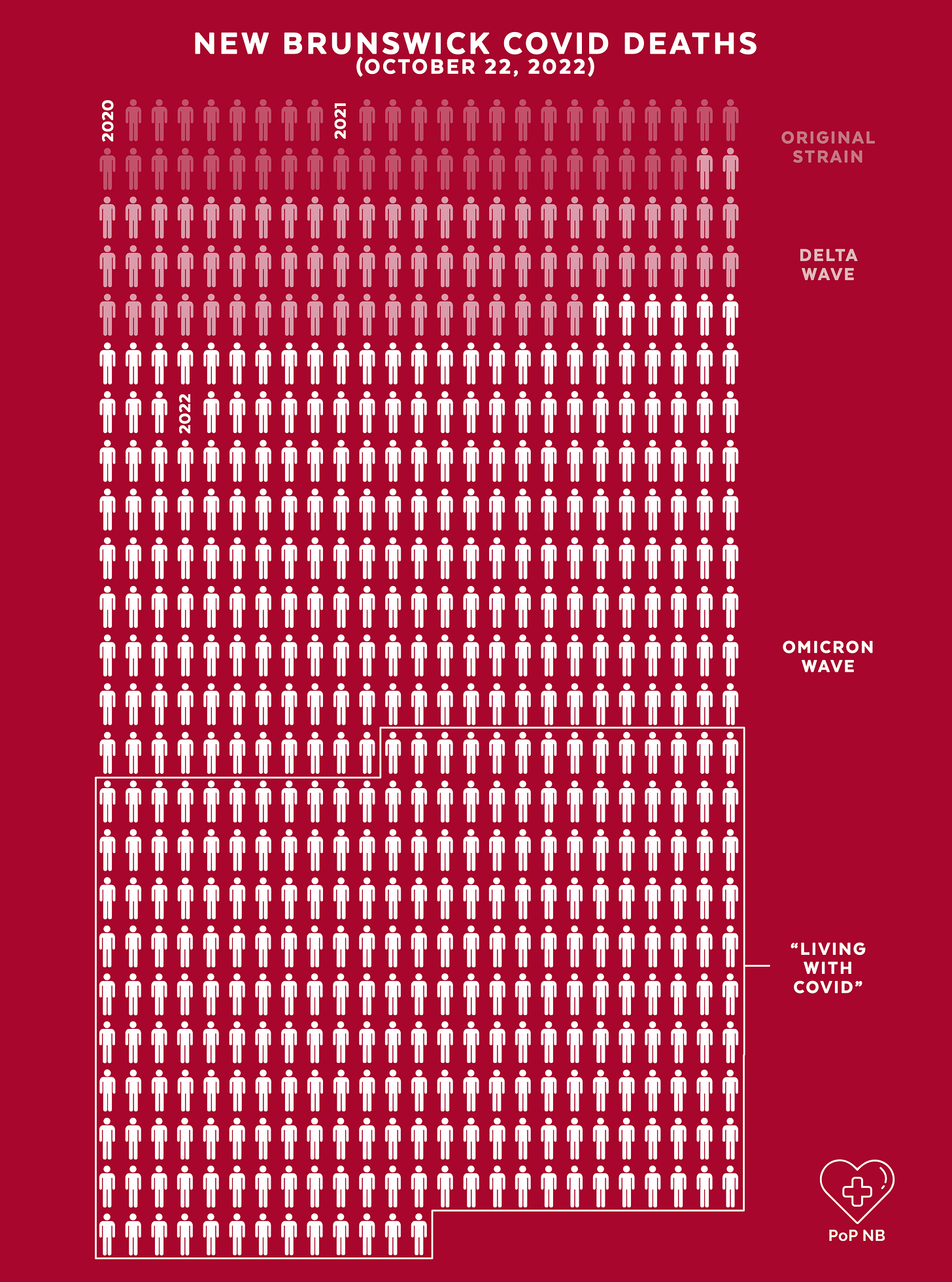
In NB "mild" Omicron is responsible for 80% of all Covid related deaths.
Long Covid can have significant and debilitating effects on daily life even if the initial infection was mild or asymptomatic. At this time, vaccination is believed, but not proven to help reduce chances of developing Long Covid.
With those considerations established, for the sake of thought experiment let's play along and see how numbers work within the concept of "the majority do not contract Long Covid" framework.
The recent Statistics Canada report puts the prevalence of Long Covid among Canadians at 14.8%. It is important to note that this is a per infection prevalence and does not take into account any increase in risk upon reinfection (believed to increase this number), or the inflated prevalence due to underreporting of cases (believed to decreased this number).
So… What are a person's chances of NOT developing long covid? Fairly good?
By the Statistics Canada estimate, on first infection, you have a 14.8% chance of developing Long Covid, or in other words, a 85.2% likelihood of not developing Long Covid. This is correct for the first instance of infection only. Each subsequent infection decreases your odds of escaping long term issues, not by nature of the disease (necessarily), but by nature of statistics.
For example, on your second infection your odds of continuing to not develop Long Covid become:
0.852 x 0.852 or 0.852² or 0.726 or 72.6%.
This is a not insignificant change to one's odds of remaining free of long term illness.
If we continue contracting Covid, as we do with influenza now, we see an ever decreasing chance of escaping the long term damage done by this disease.
Probability of escaping Long Covid in each subsequent infection looks like this:
current prob (Pc) = initial prob (Pi) ^ the number of infections (n)
The 85.2% chance of remaining free from Long Covid on your first infection becomes 72.6% upon a second infection, and 61.8% upon a third infection.
and 52.7% on fourth,
and 44.9% on fifth,
and 38.3% on sixth,
32.6% on seventh…
This is cumulative risk.
Remember that die 🎲 ?
The chance of not rolling a 1 is 83.3%. Not bad odds. Give it a try.
The chance of also not rolling a 1 on your second toss is 69.4%.
The chance of also not rolling a 1 on your third toss is 57.8%.
We understand this innately. If we continue to roll a die we will eventually get a 1, and the chances of not getting a 1 decrease with each successive roll.
The only way to ensure you do not roll a 1 is to not roll at all.
At 14.8%, Long Covid is approximately a 7-sided die.
Even in the fantasy world of "endemic" or "mild" covid, proponents of zero mitigations are damning ever increasing portions of the population (including themselves) to long term illness and disability.
Like the die toss, the only true way to avoid Long Covid is to avoid Covid.
If you would like to receive PoPNB posts in your email, please subscribe below. If you found this post helpful, please share it with your community.